Notación y nomenclatura
Al dominio también se le llama conjunto de entrada o conjunto inicial. Se denota por o
o  . A los elementos del dominio se les llama habitualmente argumento de la función.
. A los elementos del dominio se les llama habitualmente argumento de la función.Al codominio, también llamado, conjunto de llegada, conjunto final o rango de f se le denota por
Cabe señalar que el término rango es ambiguo en la literatura, ya que puede hacer referencia tanto al codominio como al conjunto imagen. Por ello, es aconsejable usar el término codominio.o codomf
Si x es un elemento del dominio al elemento del codominio asignado por la función y denotado por f(x) se le llama valor o imagen de la función f de x. Al subconjunto del codominio formado por todos los valores o imágenes se le llama imagen, alcance o recorrido de la función. Se denota por
 o
o  o
o 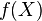 .
.Una preimagen de un
 es algún
es algún  tal que
tal que  .
.Note que puede haber algunos elementos del codominio que no sean imagen de un elemento del dominio, pero que cada elemento del dominio es preimagen de al menos un elemento del codominio.
Ejemplos
- La función definida por
 , tiene como dominio, codominio e imagen a todos los números reales
, tiene como dominio, codominio e imagen a todos los números reales 
- Para la función
 tal que
tal que  , en cambio, si bien su dominio y codominio son iguales a
, en cambio, si bien su dominio y codominio son iguales a  , sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
, sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
- En la figura se puede apreciar una función
 , con
, con
- Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,
- Esta función representada como relación, queda:


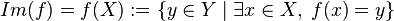


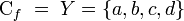

No hay comentarios:
Publicar un comentario